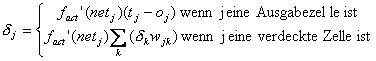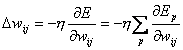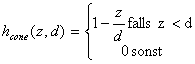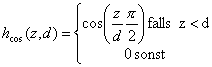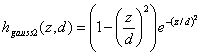1. Einleitung
Der folgende Text behandelt zuerst die Grundlagen derSimulation künstlicher neuronaler Netze, um dann anschließend auf eineAnwendung von neuronalen Netzen, die Steuerung von einem Bot, zu kommen. Eswerden nur Feedforward-Netze und Self Organizing Maps(SOM) behandelt, da nur sie beim Bot zum Einsatz kommen.
Der theoretische Abschnitt beschäftigt sich mit derMotivation bestimmte Prozesse zu simulieren und geht kurz auf die biologischen Vorbilderein. Danach folgt eine Beschreibung des Aufbaus neuronaler Netze inklusiveihrer Komponenten. Nach einer kurzen Diskussion verschiedener Ansätze desLernens folgt die Beschreibung verschiedener Lernverfahren für Feedforward-Netze,wobei der Schwerpunkt bei Backpropagation und seinen verschiedenen Abänderungenliegt. Als Beispiel für ein unüberwachtes Lernverfahren werden dieselbstorganisierenden Karten von Kohonen beschrieben.
Der 3. Teil geht auf die Realisierung der Simulation vonneuronalen Netzen auf Computern nach. Meine Simulatoren für Feedforward-Netzeund SOMs werden einzeln vorgestellt, weil sie auf verschiedenen Strukturenbasieren. Es werden die wichtigsten Datenstrukturen und ihre Funktionenvorgestellt. Gegen Ende des 3. Teils gehe ich noch einmal kurz auf dieKompromisse ein, die ich machen musste, um vernünftige Geschwindigkeiten zuerreichen. Alle Quelltexte sind in C/C++ geschrieben.
Im 4. Teil wird dann der praktische Einsatz neuronalerNetze beschrieben. Neben der Aufbereitung der Daten, die der Bot aus seiner‚Umgebung’ bezieht und der nachfolgenden Nutzung des neuronalen Netzes wird dieGewinnung von geeigneten Trainingsdaten erläutert, wie auch technischeEinzelheiten.
Anhang B beinhaltet die Quelltexte der Simulatoren und NN-relevanteTeile des Botquelltextes.
(Anmerkung: Seit dem Beginn meiner Arbeiten anmeinem Bot ist mittlerweile eine zweite und dritte Version der HPB-Templateerschienen. Mein Bot basiert auf der Version1 und ich beziehe mich in diesemText, wenn ich vom Templatecode spreche auf diese Version.)
Bots sind computergesteuerte Mitspieler in Computerspielen, die eine Mehrspieler-Unterstützung besitzen. Bots werden programmiert, damit es den Anschein hat, als ob der Spieler mit menschlichen Spielern spielt. Dies ist sonst nur auf LAN-Partys oder im Internet möglich. Ich beziehe mich in diesem Text, wenn ich von Bots spreche auf Bots für Counterstrike (CS), eine Erweiterung von Halflife (HL). HL wurde von [Valve] programmiert. 
Hier hat sich mittlerweile eine größere Gemeinde vonProgrammierern gebildet, die Bots auf der Basis von HL programmieren. Als Grundfür diese Beliebtheit ist zum einen die freie Verfügbarkeit des HalflifeQuellcodes als auch die große Beliebtheit von Counterstrike als Mehrspieler-Spielim Internet und auf LAN-Partys zu nennen. Halflife von somit auch Counterstrikesind sogenannte First-Person-Shooter, d.h. man spielt aus der Sicht einerSpielfigur in einer in diesem Fall realistischen 3D-Welt und muss Gegner mitWaffengewalt töten oder Missionsziele erreichen. Bei Counterstrike spielen 2Gruppen, die Terroristen und die Counter-Terroristen gegeneinander, wobei dieCounter-Terroristen Geiseln befreien, Bomben entschärfen müssen. DieTerroristen versuchen natürlich mit allen Mitteln dies zu verhindern. Durchdiese Aufgaben ist ein wenig taktisches Vorgehen empfehlenswert, weshalb dieseBots auch schwierig zu programmieren sind.
Gerade nach den Ereignissen am 11. September stellt sicheinem natürlich schon die Frage, ob es richtig ist, ein brutales Spiel, daszudem einen solchen Hintergrund hat, zu unterstützen, indem man es selbererweitert. CS ist in diesem Zusammenhang besonders zu nennen, da es denAnspruch erhebt, z.B. von der Wahl der Waffen realistisch zu wirken, einigeKarten, die standardmäßig mit dabei sind, eindeutig in einer arabischenUmgebung spielen und es sogar ein Spielermodel bei den Terroristen gibt, daseinen arabischen Kämpfer darstellt. Dem gegenüber sind die Spielermodels der Counter-Terroristennach dem Vorbild der SAS, der GSG-9 und den Navy Seals nachempfunden.Entscheidend für die Wahl des Spiels war damals für mich jedoch, dass dieProgrammierschnittstelle offen ist, es einige Quellen über diese gibt, und dasich mich somit nicht um die Simulation der ‚Außenwelt’ kümmern musste. Dieshatte bei vorhergehenden Projekten immer eine Menge Arbeit bedeutet. Außerdemspielte ich damals gerne CS auf LANs und war der Meinung, dass ich selbst aucheinen Bot schreiben könne, der mindestens so gut wie die damaligen Bots war,auf die ich, wenn ich CS spielen wollte, angewiesen war.
Viele der aktuellen Bots, auch meiner, basieren auf einemTemplate-Quellcode von [botman],der keine KI-Elemente enthält, aber die nötigen Funktionen zur Verbindung mitdem eigentlichen Spiel beinhaltet. Auf die technischen Realisation gehe ich inKapitel 4 ein.
Bevor man sich mit künstlichen neuronalen Netzenauseinandersetzt, ist es interessant das biologische Vorbild näher zubetrachten. Deshalb beschäftigt sich dieses Kapitel zuerst mit den biologischenUrsprüngen künstlicher neuronaler Netze, danach dann mit dem Aufbau und denLernverfahren für diese Netze.
Die Vorteile künstlicher neuronaler Netze liegen in derFehlertoleranz und der von Natur aus gegebenen Parallelität, die sie fürBerechnungen auf Parallelrechnern prädestiniert.
In biologischen Systemen übernehmen Nervenzellen dieAufgabe der Kommunikation von Zentralnervensystem und Muskeln bzw. Sinnesorganen.Der Mensch besitzt ca. 100 Milliarden Nervenzellen, wobei sich die größteAnzahl im Gehirn befindet, die Zweitgrößte im Bauchraum.
Die Nervenzellen bestehen meist aus einem Zellkörper, einemAxon und Dendriten. (Ein Spezialfall stellen die Unipolaren Nervenzellen dar,die nur ein Axon, jedoch keine Dendriten besitzen) Mit Hilfe der Dendriten,dünnen, röhrenförmigen und meist stark verästelten Fortsätzen, nimmt dieNervenzelle Reize auf. Über das Axon werden diese Impulse weitergegeben. DasEnde des Axons ist meist mehr oder weniger stark verästelt. An diesem Teil desAxons haben sich die Synapsen gebildet. Die Synapsen wandeln die elektrischenImpulse des Axons in chemische Signale um, die von anderen Nervenzellen wiederdurch ihre Dendriten aufgenommen werden können. Aber auch die Bildung vonSynapsen zwischen Dendriten oder Axonen kommt vor, wobei der Großteil aberAxone und Dendriten verbindet. Die meisten Zellen besitzen zwischen 2.000 und10.000 Synapsen, in Extremfällen auch bis zu 150.000 Synapsen. ( nach [ZellSNN97] )
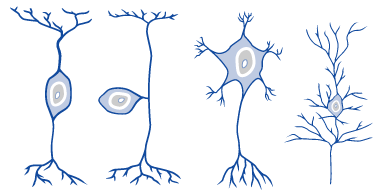
Abbildung1 :Verschiedene Arten von Neuronen. Von links nach rechts: 1. Bipolare Neuronen,um Neuronen untereinander zu verbinden; 2. Unipolare Neuronen, die sensorischeDaten übermitteln; 3. Multipolares Neuron, z.B. bei der motorischenSignalweiterleitung zu finden; 4. Ein pyramidales Neuron, das bspw. im Gehirnzu finden ist.
Bei der Betrachtung des biologischen Vorbilds der Theorienzur Simulation künstlicher Neuronaler Netze ist zu bemerken, dass es hier zweiverschiedene Ansätze gibt. T. Kohonen nennt sie in seinem Buch ( [Kohonen] ) „scholars“(engl. für Gelehrte) und „inventors“ (engl. für Erfinder). Die ‚Gelehrten’gehen mit dem wissenschaftlichen Vorsatz an das Problem heran, dass jedeTheorie durch Experimente gestützt werden können muss. Dies führt auf demBereich der künstlichen Neuronalen Netze dazu, dass sehr viele Parameter in dieFormeln zur Berechnung der Neuronen mit einfließen müssen. Auf der anderenSeite gibt es die ‚Erfinder’, die diesen Anspruch nicht haben und ein Modellmehr oder weniger erfinden und herleiten und damit evtl. auch einige Phänomenesimulieren können, obwohl sie nicht wie die ‚Gelehrten’ dem wissenschaftlichenAnspruch der Nachprüfbarkeit beim ursprünglichen Vorbild entsprechen.
KünstlicheNeuronen besitzen wie ihre biologischen Vorbilder einen oder mehrere ‚Eingänge’und einen ‚Ausgang’, zwischen denen eine meist einfache Verarbeitung desImpulse nach einfachen Regeln erfolgt.
Eine wichtige Grundlage ist, dass jeder ‚Eingang’ einesNeurons gewichtet ist, d.h. jedem ‚Eingang’ ist ein bestimmter Wert zugeordnet,der seine ‚Wichtigkeit’ bei der Verarbeitung der Daten darstellt. Dieser Wertder Verbindung von Neuron i zu Neuron j wird mit wij, dieAusgabe des Neurons i mit oi und die gesamteEingabe eines Neurons mit neti bezeichnet.
Die Berechnung der einzelnen Aktivierungen der Neuronennach dem Anlegen einer Eingabe nennt man Propagierung.
Als Gewichte werden normalerweise sowohl die Werte für dieStärke der Verbindungen wij als auch die zusätzlichauftretenden Schwellenwerte qi bezeichnet.
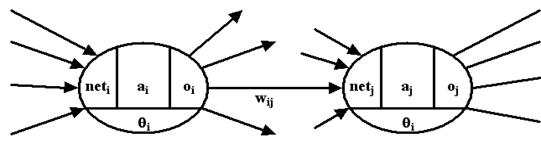
Abbildung2 : Variablender Neuronen
In Zusammenhang mit dem biologischen Vorbild sind hierviele Vereinfachungen zu nennen. Die chemischen Prozesse innerhalb der Neuronenwie bspw. der Natrium- und Kaliumionenaustausch werden nicht explizit simuliertund auch die Nachrichtenübertragung an sich wird meist vereinfacht : In derNatur kann man die Aktivität eines Neurons an dessen Frequenz mit der es feuerterkennen, während die Neuronen hier oft kontinuierliche oder auch binäre Wertebenutzen. Weiterhin werden die lokalen Nachbarschaftsbeziehungen der Neuronenuntereinander, die in der Natur u.a. durch die Diffusion von Neurotransmitternim umliegenden Gewebe stattfindet, in den meisten Modellen nicht simuliert.
Zusammenfassend kann man sagen, dass die Neuronen künstlicherneuronaler Netze meistens sehr stark vereinfacht sind und nur in Einzelfällenhalbwegs realistisch simuliert werden, was man sich dann mit dem Nachteil dersehr aufwändigen Berechnung der Netze erkauft.
Der Aktivierungszustand ai eines Neuronsist eine interne Variable, die sich aus der Netzeingabe neti unddem Schwellenwert qi mit Hilfe derAktivierungsfunktion berechnen lässt.
| | 
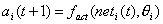
| Formel 2.1 |
Als Aktivierungsfunktion werden hauptsächlich 3verschiedene Funktionen benutzt ( nach [ZellSNN97] )
- 
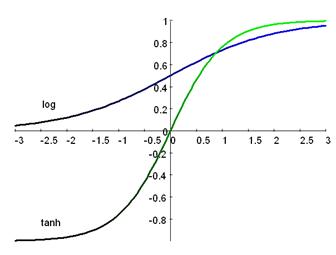Die binäre Aktivierung
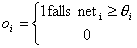
- Sigmoide Aktivierungsfunktion
o Die Logistische Aktivierungsfunktion
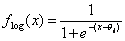bzw.mit Temperatur-Parameter T
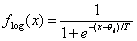
o Tangens hyperbolicus
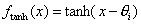
Diese Aktivierungsfunktion wird gerne in Zusammenhang mit dem LernverfahrenBackpropagation verwendet, da hier auch ein inaktives Neuron ( oi= -1) im Gegensatz zur logistischen Aktivierungsfunktion nicht 0 ist und somiteine in beide Richtungen Gewichtsänderung möglich ist.
Ineinigen Fällen wird aus simulationstechnischen Gründen der Schwellenwert durchein sogenanntes ‚on-Neuron’ ersetzt. Dieses besondere Neuron ist immeraktiviert und durch seine gewichteten und durch das Lernen veränderbarenVerbindungen zu jedem Neuron ein Ersatz für die expliziten, internenSchwellenwerte. Bei der Simulation müssen die Schwellenwerte nicht extraberechnet werden, sondern können zusammen mit den anderen Gewichten verändertwerden. Allerdings steht diesem Vorteil ein großer Nachteil gegenüber: Bei derVisualisierung der Netze werden diese leicht unübersichtlich.
Auchfür die Berechnung der Ausgabe kann es eine eigene Funktion geben, die allerdingsoft mit der Aktivierungsfunktion zusammengefasst wird.
| | 
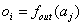
| Formel 2.2 |
DiePropagierungsfunktion bezeichnet die Vorschrift, mit der die Netzeingabeweiterverarbeitet wird
| | 
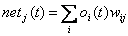
| Formel 2.3 |
Die Lernregel ist ein Algorithmus, der bestimmt, wie dasneuronale Netz lernt. Hier gibt es mehrere Ansätze, die teilweise rechtverschieden sind
Die Neuronen in einem künstlichen neuronalen Netz sindmeistens schichtweise angeordnet. Diese künstlichen Netze besitzen eine Eingabeund eine Ausgabeschicht. Um die Fähigkeiten der Netze zu erhöhen, werden oftnoch verdeckte Schichten dazwischen eingefügt. Bei der häufigsten Form, denfeedforward-Netzen sind die Ebenen meistens vollständig in einer Richtungverbunden, d.h. jedes Neuron der 1. Schicht ist jeweils mit allen Neuronen der2. Schicht verbunden. Ein Netz mit einer Eingabeschicht, einer verdecktenSchicht und einer Ausgabeschicht wird 2-stufig genannt, da es 2 Schichtentrainierbarer Gewichte besitzt.
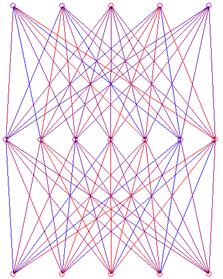
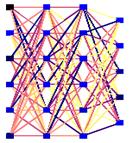
Abbildung3 : Einvollständig ebenenweise verbundenes 2-stufiges 5-7-5 Feedforward–Netz
Direkte Verbindungen zwischen der Eingabeschicht und derAusgabeschicht, also über die verdeckte Schicht hinweg, heißen shortcutconnections und sind meist ohne größere Änderungen der Simulatorarchitekturhinzuzufügen. Auch rekurrente Netze sind möglich, die jedoch größeren Aufwandin Bezug auf den Algorithmus erfordern und, für ein Ergebnis oft mehrerePropagationen benötigen und teilweise anfangen zu schwingen. Man unterscheidetvier Arten rekurrenter Netze:
- Direkte Rückkopplung
Durch die direkte Rückkopplung können sich die Neuronen selbst hemmen bzw.aktivieren und somit kleine Eingangssignale in bestimmten Bereichen verstärken.
- Indirekte Rückkopplung
Verbindungen von höheren Schichten zu niedrigeren können beispielsweise zurAufmerksamkeitssteuerung eingesetzt werden. Hierbei wird die ursprünglicheEingabe verarbeitet und mit einer Ausgabe assoziiert, die wieder dazu benutztwerden kann, bestimmte Eigenschaften der Eingabe besonders zu beachten.
- Rückkopplung innerhalb einer Schicht.(lateral feedback)
Die Rückkopplung innerhalb einer Schicht wird oft dann eingesetzt, wenn nur einNeuron in der gesamten Schicht aktiv sein soll. Um das zu erreichen, hemmenalle Neuronen alle anderen Neuronen und versuchen sich selbst noch weiter zuaktivieren. Das Neuron mit der ursprünglich höchsten Aktivierung bleibt am Endeals Gewinner, während alle anderen Neuronen nicht mehr aktiviert sind. Deshalbheißen solche Netztopologien auch winner-takes-all Netzwerke.
- Vollständig verbundene Netze
Bei vollständig verbundenen Netzen ist jedes Neuron mit jedem Neuron verbunden.Bekanntester Vertreter dieser Art sind die Hopfield-Netze, die beiOptimierungsproblemen wie dem Travelling-Salesman-Problem eingesetzt werdenkönnen.
( nach [ZellSNN97] )
Die Lernfähigkeit neuronaler Netze ist eine der speziellenEigenschaften neuronaler Netze. Sie benötigen dafür eine Eingabe und meistensauch eine Ausgabe, mit deren Hilfe sie ihre internen Zustände wieSchwellenwerte und Gewichte verändern, um der „erwünschten“ Ausgabe möglichstnahe zu kommen. Wenn sie einmal einen Trainingsdatensatz gelernt haben, sindsie auch in der Lage unbekannte Eingaben so zu verarbeiten meist und einpassendes Ergebnis zu erzeugen.
Das Lernen kann bei neuronalen Netzen durch Veränderung derGewichte, also der Gewichtungen der Verbindungen und der Schwellenwerte, dasErstellen oder Löschen von Verbindungen oder Neuronen erfolgen. In der Praxiswerden fast immer nur die Gewichte verändert.
Man unterscheidet 3 Arten des Lernens:
Beim überwachten Lernen werden dem Netz von außen sowohlEingabe, als auch die zugehörige gewünschte Ausgabe präsentiert. Die Aufgabedes Lernalgorithmus besteht darin, die Gewichte und Schwellenwerte so zuverändern, dass nach mehrmaliger Präsentation der Muster das Netz in der Lageist, zu einer Eingabe die passende Ausgabe zu liefern. Nach dem Lernprozess istdas Netz dann auch in der Lage für neue, unbekannte Eingabevektoren einegeeignete Ausgabe zu finden. Diese Eigenschaft, die Generalisierungsfähigkeit,ist eine wichtige Eigenschaft neuronaler Netze, da ihnen meist nicht allemöglichen Eingaben mit den entsprechenden Ausgaben von vornherein präsentiertwerden können.
Ein Nachteil des Überwachten Lernens ist, dass esbiologisch nicht plausibel ist, weil in biologischen Systemen keine Institutionexistiert, die Eingaben zusammen mit der gewünschten Ausgabe liefert.
Beispiel für den Ablauf eines überwachten Lernprozesses:
- Präsentation der Eingabe durchentsprechende Aktivierung der Neuronen der Eingabeschicht
- Propagierung des Netzes, sodass eineAusgabe erzeugt wird
- Vergleich der Ausgabe mit dergewünschten Ausgabe
- Bei Netzen mit mehreren Schichten:Rückwärtspropagierung der Fehler der Ausgabeschicht zu Neuronen in verdecktenSchichten.
- Änderung der Gewichte, um den Fehler zuminimieren
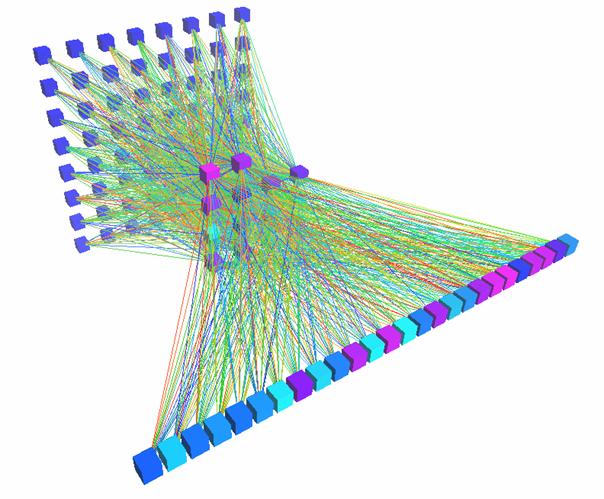
Abbildung4 : Ein64-14-26 feedforward Netz, das ich mit Hilfe des überwachten LernverfahrensBackpropagation zur Erkennung von großen Druckbuchstaben verwendet habe. ( dieFarben der Verbindungen stellen das Gewicht, die der Neuronen derenSchwellenwert dar )
Beidiesem Lernverfahren wird dem Netz zusammen mit der Eingabe nicht der kompletteAusgabevektor, sondern nur wenige Informationen, richtig / falsch oder auch derGrad des Fehlers, präsentiert. Dieses Verfahren ist auch biologisch plausiblerals überwachtes Lernen, da Vorgänge wie ‚Erfolg’ oder ‚Misserfolg’ auch in derNatur zu finden sind. Allgemein ist dieses Verfahren jedoch sehr zeitaufwändig,da dem Netz nur wenige Informationen zur Verfügung stehen.
2.3.3 Unüberwachtes Lernen(Unsupervised Learning)
BeimUnüberwachten Lernen werden dem Netz eine Trainingsmenge von Eingabevektorenpräsentiert, die es ohne direkte Vorgaben von außen in Gruppen einteilt. Diebekanntesten Netze, die nach einem Unüberwachten Lernverfahren arbeiten, sinddie Selbstorganisierenden Karten (Self Organizing Maps).Bei SOM beeinflussen aktive Neuronen ihre räumlich nahen Nachbarneuronen undbewirken damit, dass sich ähnliche Muster an bestimmten Stellen ‚sammeln’,Gruppen bilden. Den SOMs ähnliche Strukturen wurden im visuellen Kortex vonSäugetieren gefunden, sodass diese Modelle auch biologisch plausibel sind. Diefür dieses Lernverfahren nötige Suche nach dem am stärksten aktivierten Neuronwird allerdings bei der Simulation fast immer durch eine einfache Maximumsucherealisiert, da ein rekurrentes Netz, das die gleiche Aufgabe erfüllen soll,immer mehr Zeit benötigt, einen stabilen Punkt zu erreichen, bzw. keinenfindet, also ständig oszilliert.
Beispiel für den Ablauf eines unüberwachten Lernprozessesam Beispiel von SOM:
- Präsentation der Eingabe durchentsprechende Aktivierung der Eingabeneuronen
- Propagierung
- Suche nach dem am stärksten aktiviertenNeuron ( winner-takes-all)
- Änderung der Gewichte anhand derEntfernung vom zu aktualisierenden Neuron zum Gewinnerneuron
( nach [ZellSNN97] )
AlsFeedforward-Netze werden neuronale Netze bezeichnet, bei denen die Eingabe nur inRichtung der Ausgabeschicht propagiert wird.
h ist in den folgenden Fällen alsLernrate definiert, also eine Variable, die die Geschwindigkeit mit der dieGewichte verändert werden, angibt. Wird h zu klein gewählt, dauert dasTraining unnötig lange und es findet in lokalen Minima einen stabilen Punkt.Wird die Lernrate jedoch zu groß gewählt, kann es vorkommen, dass derLernvorgang nicht optimal verläuft.
Die Hebb-und Deltaregeln gelten nur für einstufige Netze.
DieHebbsche Lernregel ist die Grundlage für viele andere Lernregeln. Sie besagt,dass wenn zwei verbundene Neuronen stark aktiviert sind, das Gewicht derVerbindung erhöht werden soll.
| | 
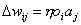
| Formel 2.4 |
DieseLernregel wird meistens bei binären Aktivierungsfunktionen benutzt, wobei oft jedoch–1 und 1 als Aktivierungen verwendet werden, um auch eine Verminderung derBeträge der Gewichte zu ermöglichen.
Beidieser Lernregel ist die Veränderung proportional zur Differenz d vonpropagierter Ausgabe oi(Ausgaben der Neuronen derAusgabeschicht) von gewünschter Ausgabe ti. Dies ist eineErweiterung der Hebbschen Lernregel, wobei auch die propagierte Ausgabe bei derÄnderung beachtet wird.
| | 
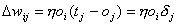
| Formel 2.5 |
ist hierder Fehler des Ausgabeneurons j.
DieDelta-Regel ist außerdem ein Sonderfall, der bei 1-stufigen Netzen auftritt,von dem nun folgenden Lernverfahren Backpropagation.
DasLernverfahren Backpropagation (BP) ist eine Verallgemeinerung der Delta-Regelfür mehrstufige Netze. Hierbei wird der Fehler, der in der Ausgabeschichtdirekt berechnet werden kann, zurückpropagiert, d.h. es werden alle Fehler derNeuronen, mit denen das betreffende Neuron in einer höheren Schicht verbundenist, unter Beachtung der Gewichte der entsprechenden Verbindungen, addiert. Dadie Aktivierungsfunktion bei der Vorwärtspropagierung und somit auch bei derRückwärtspropagierung eine Rolle spielt, muss auch sie mit in die Rechnungeinbezogen werden.
Backpropagation :
| | 
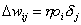
| Formel 2.6 |
| | 
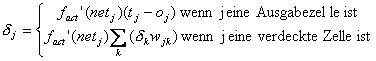
| Formel 2.7 |
Backpropagationist ein sogenanntes Gradientenabstiegsverfahren. Wenn man sich die Fehlerflächeeines neuronalen Netzes bildlich vorstellt, so sucht dieses Verfahren stets denkürzesten Weg ins Tal. Dies tut es indem es sich entgegen der Steigung andieser Stelle bewegt. Die Fehlerfläche eines Netzes ist aber nicht 2dimensional, sondern hat so viele Dimensionen wie es Gewichte gibt. ( InAnlehnung an [ZellSNN97])
DieGesamtfehlerfunktion ist wie folgt definiert :
| | 
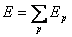
| Formel 2.8 |
Hierbei ist p der Index für die einzelnen Trainingsmuster.Für einzelne Muster lautet sie :
| | 
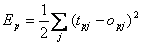
| Formel 2.9 |
Da man das Minimum finden will, muss man die Gewichteentgegen dem Gradienten verändern.
| | 
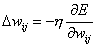
| Formel 2.10 |
Hier begegnet uns wieder h, die Lernrate, dieangibt, wie schnell die Gewichte verändert werden sollen. Nun muss dieAbleitung der Fehlerfunktion berechnet werden. Zuerst werden wir die Herleitungder Delta Regel betrachten, die einen Sonderfall von Backpropagation darstellt.In diesem Fall gilt :
| | 
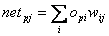
| Formel 2.11 |
| | 
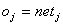
| Formel 2.12 |
Die Änderung der Gewichte über alle Muster ist dann :
| | 
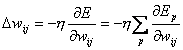
| Formel 2.13 |
Mit der Kettenregel folgt :
| | 
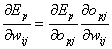
| Formel 2.14 |
Aus der Gleichung für die Fehlerfunktion einzelner Muster folgt:
| | 
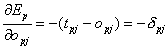
| Formel 2.15 |
Nun muss noch opj nach wij abgeleitetwerden :
| | 
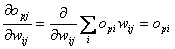
| Formel 2.16 |
Zusammengefasst lautet oberes dann :
| | 
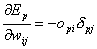
| Formel 2.17 |
Insgesamt ergibt sich somit für die Delta Regel :
| | 
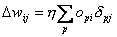
| Formel 2.18 |
Man erkennt dass es sich hierbei um ein offline oder batch-Trainingsverfahrenhandelt. Ein gravierender Nachteil dieses Verfahrens ist, dass man extraDatenelemente benötigt, die die aufsummierte Änderung speichert. Ein weitererNachteil ist, dass man von vornherein alle Trainingsdaten benötigt. Aus diesenGründen verwendet man in der Praxis oft die Online-Variante, d.h. eine Variantedie die Gewichte jeweils nach der Präsentation eines Musters ändert.
| | 
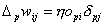
| Formel 2.19 |
Backpropagation stellt nun eine Art Erweiterung der DeltaRegel für neuronale Netze mit mehreren trainierbaren Schichten von Gewichtendar.
In in dieser Weise aufgebauten Netzen ist die Berechnungdes Fehlers ![]()
nicht mehr so einfach wie im Falle dereinschichtigen neuronalen Netze. Man hat keine ‚Sollwerte’ für die Neuronen derverdeckten Schicht(en). Aus dieser Tatsache resultiert, dass der Fehler derAusgabeneuronen zurückpropagiert werden muss um diesen fehlenden Wert zu bekommen( womit auch dann der Name des Lernverfahrens geklärt ist ).
Zusammenfassend noch einmal die Propagierungsregeln, aufdie später wieder zurückgegriffen werden muss :
| |
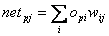
| Formel 2.20 |
| | 
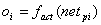
| Formel 2.21 |
Analog zu der Herleitung der Delta Regel gilt wieder :
| | 
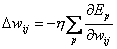
| Formel 2.22 |
Auch hier kann man den abzuleitenden Term mit Hilfe derKettenregel erst einmal zerlegen :
| | 
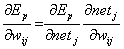
| Formel 2.23 |
Der zweite Term ist dann ( mit 2.20 ) :
| | 
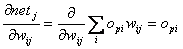
| Formel 2.24 |
Und der Fehler eines Neurons wird auch wie bei der DeltaRegel definiert ( 2.15 ):
| | 
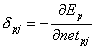
| Formel 2.25 |
Wenn man jetzt die Formeln ( 2.22, 2.23, 2.24, 2.25) zusammenfasst, erhält man
| |
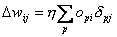
| Formel 2.26 |
oder in der online Version :
| |
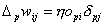
| Formel 2.27 |
wie bei dem oben hergeleiteten Lernverfahren, mit demUnterschied, dass ![]()
aus den oben genannten Gründenkomplizierter zu berechnen ist. Und auch hier hilft die Kettenregel wieder weiter:
| | 
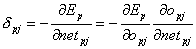
| Formel 2.28 |
Aus Gleichung ( 2.21 ) folgt :
| | 
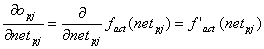
| Formel 2.29 |
Nun muss man bei den Neuronen zwischen verdeckten Zellenund Ausgabeneuronen unterscheiden. Im ersten Fall gilt wieder das Gleiche wiebei der Delta Regel :
| | 
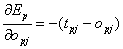
| Formel 2.30 |
Im zweiten Fall kann man den Term mit Hilfe der Gleichungen( 2.20, 2.25 ) lösen :
| | 
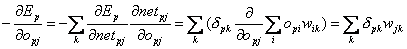
| Formel 2.31 |
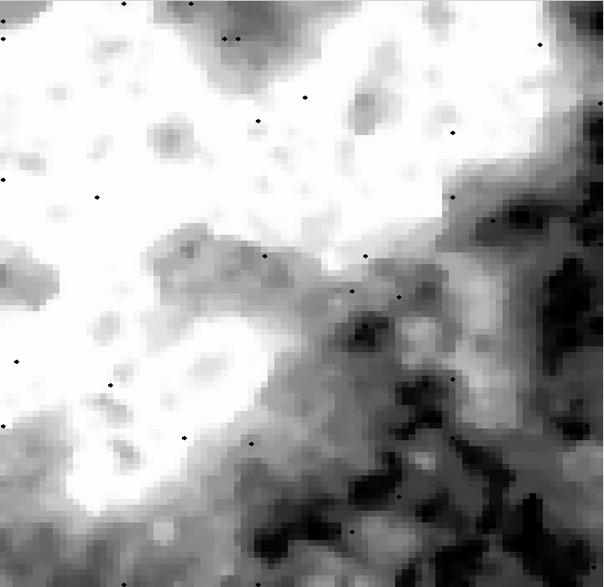
Abbildung5 : Das 2Spiralen Problem, ein beliebtes Benchmarkverfahren um die Leistungsfähigkeiteines Lernalgorithmus zu testen. Ein neuronales Netz, das aus zwei Eingabe-,einer unbestimmten Anzahl Schichten verdeckter Neuronen und einem Ausgabeneuronaufgebaut ist, soll anhand der Position eines Punktes, die als Eingabevorgelegt wird, entscheiden, zu welcher der beiden Spiralen dieser Punktgehört, durch die schwarzen und weißen Punkte auf der rechten Seitesymbolisiert.
Füreinige Trainingsmuster sind Abänderungen teilweise vorteilhaft. Eine solcheErweiterung ist der Momentum-Term. Dieser Term beachtet die letzteGewichtsänderung bei der neuen Berechnung. Er bewirkt eine Beschleunigung der Gewichtsänderungenauf weiten Plateaus der Fehlerfläche und bremst in zerklüfteten Gebieten ab, dahier die ‚alten’ Gewichtsänderungen oft ein anderes Vorzeichen haben.
Gängige Werte für a liegen zwischen 0.5 und 0.9,wobei dieser Wert jedoch auf die einzelnen Trainingsmuster angepasst werden.
| | 
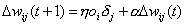
| Formel 2.32 |
EinProblem ist, dass sich Neuronen bei den oben beschriebenen Verfahren in denextremen Aktivierungsbereichen nur langsam ändern können. Die Ursache liegt beider Ableitung der Aktivierungsfunktion, die bei der Fehlerberechnung benutztwird. In diesen Bereichen ist die hat die Ableitungsfunktion einen Wert nahe 0.Um dieses Verhalten zu verbessern kann man zu jedem Wert der Ableitung einenfesten Wert (0.1 genügt oft schon) addieren. Auch eine feste Zuweisung verbessertteilweise die Konvergenz des Netzes, die variable Variante ist jedoch meistschneller.
Ineigenen Versuchen mit einem 10-5-10 De/Encoder konnte ich eine 40% Senkung der zutrainierenden Epochen mit dieser Variante gegenüber der unveränderter Ableitungerreichen.
![]()
Abbildung6 :Funktionsgraph der Ableitung der Aktivierungsfunktion ohne ( g(x) ) und mitFlat Spot Elimination ( h(x) ). In den roten Bereichen, den extremenAktivierungsbereichen, wird g(x) sehr klein und somit werden auch dieVeränderungen während des Lernvorgangs sehr klein, da fact(netj)als Faktor bei der Berechnung der Fehler der einzelnen Neuronen vorkommt. Somit ist es für ein Neuron, das sich in einem solchen Bereich befindet, diesennur langsam wieder zu verlassen. Wenn man zu dieser Funktion immer einenfesten Wert hinzuzählt oder auch diese auf einen festen Wert setzt, sindüberall ausreichende Gewichtsänderungen möglich. ( h(x) )
SelbstorganisierendeKarten sind aus einer Eingabeschicht und einer Schicht aktiver Neuronenaufgebaut und werden mit einem unüberwachten Lernverfahren trainiert. DieNeuronen besitzen untereinander Nachbarschaftsbeziehungen, und sie sind ineinem n-dimensionalen Gitter angeordnet. Um die Visualisierung zu vereinfachen,werden meist rechteckige oder teilweise auch hexagonale 1,2 oder 3 - dimensionaleGitter benutzt. [Kohonen]
DieNeuronen der aktiven Schicht besitzen jeweils einen Gewichtsvektor Wj,der so viele Dimensionen hat, wie der Eingabevektor E.
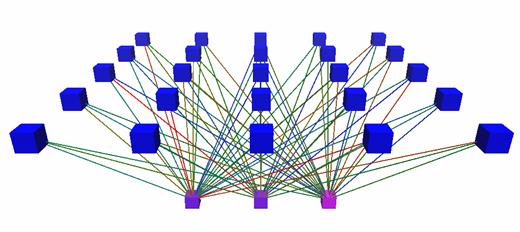
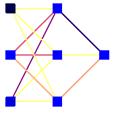
Abbildung7 :Prinzipieller Aufbau einer SOM. Unten sind die 3 Eingabeneuronen, oben die 25Neuronen, die die eigentliche selbstorganisierende Karte darstellen. In der Naturbesitzen ähnlich aufgebaute Netze noch laterale rekurrente Verbindungen, inSimulatoren, werden diese jedoch oft durch eine Maximumsuche ersetzt. Auch dieEingabeneuronen existieren nicht immer explizit in den Simulatorstrukturen, dadie eigentlichen Bestandteile des Netzes die, in diesem Fall, oberen Neuronensind.
DasLernen läuft so ab, dass dem Netz zuerst ein Trainingsmuster präsentiert wird.Danach folgt eine Art Propagierung, allerdings keine Berechnung einzelnerAktivierungen aus Schwellenwert und Netzeingabe, sondern eine Suche nach demkleinsten Unterschied zwischen Eingabe und Gewichtsvektor eines Neurons. ZumVergleich werden meist die euklidische Norm oder das Skalarprodukt beinormalisierten Vektoren verwendet. Danach werden die Gewichtsvektoren zumEingabevektor hin verändert, wobei mit steigendem Abstand die Stärke derVeränderungen abnimmt.
| | 
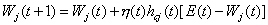
| Formel 2.33 |
| | 
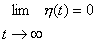
| Formel 2.34 |
| | 
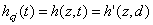
| Formel 2.35 |
| | 
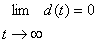
| Formel 2.36 |
h(t) ist die zeitlich veränderliche Lernrate. Normalerweiseverwendet man eine monoton fallende Funktion, aber auch mit festen Werten habeich brauchbare Ergebnisse erzielt. hcj(t) ist dieDistanzfunktion. (neighbourhood kernel) c in diesem Fall dasGewinnerneuron, j das aktuelle Neuron und z die Distanz zwischenbeiden. hcj(t) ist auch eine monoton fallende Funktion. Beiihrer Berechnung wird der interne Wert d(t), der Distanzparameter, derden Radius darstellt in dem die Gewichte der Neuronen verändert werden, mitverwendet. d ist am Anfang des Training oft so groß, dass die Gewichtealler Neuronen ausreichend stark verändert werden. [Kohonen]schlägt sowohl für h(t) als auch für hcj(t)lineare Funktionen vor. Ich habe auch gute Erfahrungen mitExponentialfunktionen gemacht, habe allerdings beobachtet, dass man dann mehrEpochen benötigt um das Netz gut trainiert zu haben.
Beispiele für gängige Nachbarschaftsfunktionen mit[0,1]:
| | 
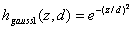
| Formel 2.37 |
| | 
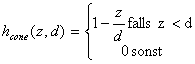
| Formel 2.38 |
| | 
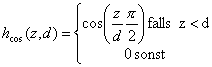
| Formel 2.39 |
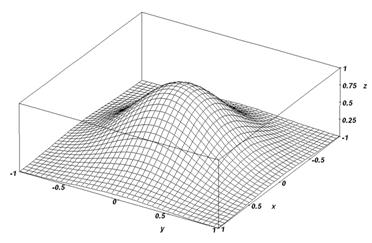
Abbildung 8 : DieNachbarschaftsfunktion hgauss1
Beispiel für eine Nachbarschaftsfunktion mit [-1,1]:
| | 
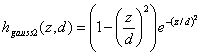
| Formel 2.40 |
Man könnte denken, dass eine solche Karte sich schnellerentfaltet, da alle weit entfernten Neuronen ‚abgestoßen’ werden. Dieser Falltritt jedoch nicht ein, sondern die Karte dehnt sich so stark aus, dass keinevernünftigen Klassifikationen mehr erreicht werden können. Auch mit sog.Mexican-Hat Funktionen, also zur y-Achse symmetrische Funktionen, die mitgrößeren x-Werten erst von 1 auf einen negativen Wert absinken um sich dann dery-Achse anzunähern, habe ich solche Effekte beobachtet.
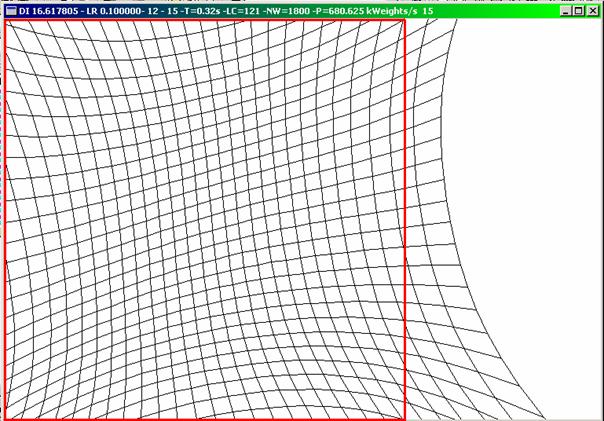
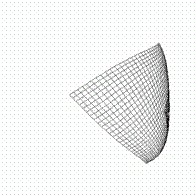
Abbildung9 : Eine‚explodierende’ Karte nach 15 Epochen, die hgauss2 benutzte. Die rotenLinien zeigen die Grenzen des Eingaberaums. Nach weiteren Epochen waren nurnoch wenige Neuronen sichtbar.
Beispiel einer Entfaltung einer Karte:
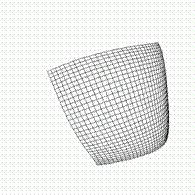
Abbildung10 :Entfaltung einer Karte (Sx = 30; Sy=30) nach dem Trainingvon 0,5,10,20,40,69 Epochen (;) eines das Quadrat gleichmäßig abdeckenden Datensatz. (Epoche -> 1 Präsentation aller zu lernender Datensätze)
| 
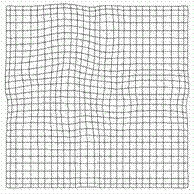
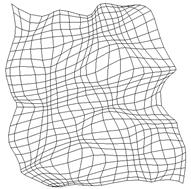
Abbildung 11 : Endform eines Netzes, das mit einer konstanten Lernrate trainiert wurde und die oben genannten Merkmale zeigt. |
Wennder Parameter d zu klein initialisiert wird, oder zu schnell absinkt, kann esvorkommen, dass sich weiter entfernte Neuronen nicht mehr beeinflussen könnenund somit nur Teilbereiche korrekt klassifiziert werden können. Diesen Effektnennt man topologischen Defekt.
Wenn die Lernrate nicht schnell genug abfällt oderkonstant ist, kann es vorkommen, das einzelne Neuronen sich noch kurz vor Endedes Trainings zu den ihrem Gewichtsvektor nahe liegenden Trainingsmustern indiese Richtung verändern. Man erhält dann kein ‚glattes’ Bild, sondern einigeNeuronen scheinen aus ihren Reihen gezogen worden zu sein.
| 
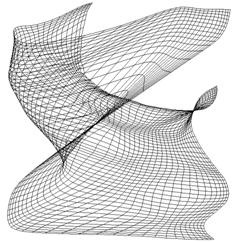
Abbildung 12 : Ein topologischer Defekt (bzw. eigentlich sogar zwei Defekte) |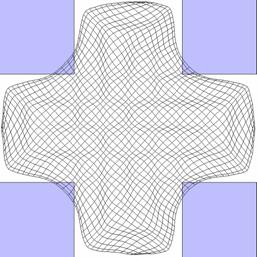 
Abbildung 13 : Eine Karte, die einen kreuzförmigen Eingabebereich abbildet. Sie hat keine topologischen Defekte. |
Bei den beiden nachfolgend vorgestellten Simulatorenhandelt es sich um 2 vollkommen getrennte Programme, die auch verschiedenaufgebaut sind.
Dieser Simulator simuliert Feedforward-Netze, die mitBackpropagation oder seinen Modifikationen Momentum und Flat Spot Eliminationtrainiert werden. Auch Time Delay NN (TDNN) werden unterstützt. Der Simulatorist so ausgelegt, dass auch während des Trainings ohne Probleme Neuronen undVerbindungen hinzugefügt werden können. Neben den bereits existierendenAktivierungsfunktionen können auch eigene eingebunden werden.
Alle mit diesem Simulator gewonnen Daten können in Dateiengespeichert werden. Normalerweise ist dies ein Binärformat, Trainingsdatenkönnen aber auch in einem für Menschen lesbaren Format gespeichert werden.
Es gibt eine einfache im Aufbau befindliche beschreibendeSprache, wobei allerdings bis jetzt Trainingsmuster in Dateien vorliegen müssenund nicht innerhalb der Sprache generiert werden können.
Tabelle 1 : Hauptklassen desSimulators für Feedforward-Netze
| Klasse | Bedeutung / Funktion | Dateien |
| NeuronBase | Dieser Datentyp beinhaltet alle grundlegenden Variablen eines Neuronen in einem Feedforward-Netz. Neben den Variablen für die Aktivierung, dem Schwellenwert, dem zurückpropagierten Fehler, der Netzeingabe, der Position im Netz und Zeiger auf die Aktivierungsfunktion und ihre Ableitung gibt es je eine Liste mit Zeigern auf die mit diesem Neuron verbundenen Neuronen und Indices für die dazugehörigen Gewichte. Es gibt eine Liste für die Neuronen, von denen Signale kommen und zu denen Signale ‚gesendet’ werden. | NeuronBase.h |
| NeuronBProp | Dieser Datentyp ist vom Datentyp NeuronBase abgeleitet. Er erweitert ihn um die Propagierungsfunktion und die Funktion zur Berechnung des Fehlers d. | NeuralNetBProp.h NeuralNetBPropDef.h |
| LinkBase | Eine Datenstruktur, die einen Zeiger auf ein Neuron und einen Index für das dazugehörige Gewicht in der Liste der Gewichte enthält. | LinkBase.h LinkBaseDef.h |
| WeightBase | Diese Klasse besitzt einen Zahlenwert für das Gewicht und einen Zähler für die Anzahl der Benutzungen in einem Netz, um gekoppelte Gewichte zu ermöglichen. | WeightBase.h WeightBaseDef.h |
| WeightBProp | Dieser Datentyp ist von WeightBase abgeleitet, aber hat keine Funktionen oder Variablen, die ihn erweitern | NeuralNetBProp.h NeuralNetBPropDef.h |
| NeuralNetBase | Basisklasse für alle in diesem Simulator verwendeten Typen neuronaler Netze. Sie liefert Versionsinformationen und definiert mit Hilfe rein virtueller Funktionen, welche Funktionen in einer abgeleiteten Klasse implementiert werden müssen. Zudem enthält sie Funktionen zur Berechnung der Gesamtfehler des Netzes. | NeuralNetBase.h NeuralNetBaseDef.h |
| NeuralNetBProp | Klasse, die ein vollständiges NN beinhaltet. Ein Feld enthält die Listen der Neuronen auf jeweils einer Schicht. Außerdem sind alle Gewichte der Verbindungen in einer Liste gespeichert. | NeuralNetBProp.h NeuralNetBPropDef.h |
(Allerelevanten Klassen besitzen Funktionen, die das Speichern der Daten in Dateienunterstützen)
DieKlassen NeuralNetBPropM für Backpropagation mit Momentum-Term und NeuralNetTDNNBPropMfür Time Delay Neural Networks mit Momentum-Term sind größtenteils mit NeuralNetBPropidentisch. Der gesamte Simulator ist in C++ geschrieben, jedoch habe ich nichtganz streng objektorientiert, was man daran sieht, dass NeuralNetBPropM nichtvon NeuralNetBProp abgeleitet ist. Als ich den Simulator geschrieben habe, habeich diesen Aufbau aus Performancegründen gewählt.( Dies wäre sicherlich durchZeiger die auf erweiternde Datenelemente zeigen oder durch Anwendung vonPolymorphismus zu lösen gewesen, jedoch hatte ich zu dem Zeitpunkt noch nichtdie nötige Erfahrung. ) Ein großer Teil der Arbeit an dem Simulator bestanddarin, die Geschwindigkeit zu optimieren. Mit Hilfe vieler Veränderungen war esdann letztendlich möglich, die Geschwindigkeit von ungefähr einem kCUPS auf zwei MCUPS zu steigern.
DieGewichte der Verbindungen des neuronalen Netzes werden in einer Listegespeichert, die Verbindungen besitzen nur einen Gewichtsindex. Die Gewichteals oft benutzte Daten liegen so zusammen und können schnell erreicht werden.
AmAnfang der Entwicklung des Simulators benutzte ich noch einfach verketteListen. Diese Listen hatten jedoch bei einer größeren Länge den Nachteil, dasssie extrem langsam wurden. Daraufhin habe ich eine Listenklasse entwickelt, dieauf verketteten Feldern basiert. Dieser Ansatz hat zwar den Nachteil, dass oftviel Speicher reserviert wird, dafür aber umso schneller ist. Man kann dieGröße der Felder in der Liste anpassen, sodass man ein Mittelmaß zwischenSpeichernutzung und Geschwindigkeit finden kann. Eine Festlegung derSchichtgrößen der Netze von vornherein, bzw. bei Anfang des Trainings wollteich nicht vornehmen um auch während des Trainings das einfache Hinzufügen vonNeuronen und Verbindungen zu ermöglichen (zur einfachen Realisierung vonCascade-Correlation, einem Lernverfahren, dass auf dem Verändern von Gewichtenbei gleichzeitigem Hinzufügen von Neuronen basiert). Als Feldgrößen bieten sich2er Potenzen an, da diese von den meisten Compilern als einfacheVerschiebeoperationen übersetzt werden, die wesentlich schneller als Divisionenoder Multiplikationen und Verschiebungen auszuführen sind.
Tabelle 2 : Beispiele für dieBerechnung der Nummer des Feldes bei gegebenem Index des zu suchenden Objektsbei verschiedenen Feldgrößen
| Berechnung mit Hilfe des Verschiebeoperators SAR und SHL, der 3 Zyklen benötigt (Feldgröße 210 = 1024) | |
| mov esi, DWORD PTR [ebx+8] cdq and edx, 1023 push edi add eax, edx mov edi, ecx sar eax, 10 mov edx, eax shl edx, 10 sub edi, edx | mov eax, 628292359 dec ecx push ebp imul ecx sar edx, 7 mov eax, edx push esi shr eax, 31 add edx, eax mov esi, DWORD PTR [ebx+8] push edi mov edi, ecx lea eax, DWORD PTR [edx*8] sub eax, edx lea eax, DWORD PTR [eax+eax*4] lea eax, DWORD PTR [eax+eax*4] lea eax, DWORD PTR [eax+eax*4] sub edi, eax |
Tabelle 3 : Hauptklassen des SOMSimulators
| Klasse | Bedeutung / Funktion | Dateien |
| nVec | Dieser Datentyp ermöglicht das Rechnen mit n-dimensionalen Vektoren, wie sie bei der Simulation von SOMs benötigt werden. Diese Klasse beinhaltet Funktionen zur Addition, Subtraktion, Normalisierung und Streckung. Außerdem wurde ein spezieller Mechanismus implementiert, der es erlaubt, auf Datensätze zuzugreifen, ohne sie zeitaufwändig kopieren zu müssen. | nVec.h nVec.cpp nVecErr.h |
| qSOM2d | Diese Klasse ist der Datentyp, der die Daten und Funktionen zur Simulation Self Organizing Maps bereitstellt. Die Schnittstelle wurde auf möglichst wenige Funktionen beschränkt. Durch sie können die Lernrate, der Distanzparameter, das aktuelle Gewinnerneuron und einzelne Gewichtsvektoren abgefragt bzw. festgesetzt werden. | CqSOM2d.h CqSOM2d.cpp NSOMErr.h |
| SOMPattern | Diese Klasse verwaltet Trainingsdaten für SOMs. Sie können manipuliert und als Datei gespeichert werden. | SOMPattern.h SOMPattern.cpp |
(Allerelevanten Klassen besitzen Funktionen, die das Speichern der Daten in Dateienunterstützen)
DieKlasse qSOM2d beinhaltet ein Feld Zeiger auf die Gewichtsvektoren vom Typ nVec.Die Klasse SOMPattern greift über einen internen Zeiger, der einmal zurLaufzeit gesetzt werden muss, auf die Klasse qSOM2d zu, um bspw. eine Epoche zutrainieren. Die Trainingsdaten werden in der Klasse SOMPatternElem gespeichert,die selbst von nVec abgeleitet ist. Während des Trainings werden zusätzlich dieKategorisierungsfehler in einer Variable innerhalb von SOMPatternElemgespeichert, um im Nachhinein eine Aussage über das Lernverhalten der Karte inBezug auf bestimmte Datensätze machen zu können.
qSOM2dbesitzt als Besonderheit zwei Funktionen zur Kategorisierung von Eingabedaten :qSOM2d::Categorize und qSOM2d::CategorizeFast. Die erste Funktion geht alleNeuronen durch, berechnet ihren Abstand zum Gewinnerneuron und passt dieGewichte entsprechend an. Die zweite Funktionen zur Kategorisierung berechnetnur die Neuronen, die sich innerhalb eines Quadrates, dessen Seitenlänge doppeltso groß ist wie der Distanzparameter, und dessen Mittelpunkt im Gewinnerneuronliegt, befinden. Diese Funktion ist bei den Nachbarschaftsfunktionen gutanzuwenden, bei denen der Funktionswert 0 ist, wenn die Distanz größer als derDistanzparameter ist. Bei der sonst gut konvergierenden Nachbarschaftsfunktionfgauss1 ist diese beschleunigte Funktion meiner Erfahrung nach nichtohne eine Verschlechterung der Kategorisierung anzuwenden.
In denoben genannten Funktionen ist noch eine technische Besonderheit zu beobachten :Die Neuberechnung der Gewichte erfolgt nicht mit einer lokalen Kopie der Datendes zu verändernden Gewichts, sondern direkt im Speicher. Dies wird dadurcherreicht, dass die entsprechende Instanz von nVec nicht selber Speicherallokiert, sondern nur einen Zeiger auf die Position der Daten im Speicher undeine entsprechende interne Variable setzt, um später nicht zu versuchen diesenSpeicher im Destruktor wieder freizugeben.
4. Praktischer Einsatz derNeuronalen Netze im Bot
Das neuronale Netz des Bots wird (bis jetzt)offline, d.h. außerhalb des Spiels, trainiert. Ein online-Training wäre zwarrein zeitlich möglich, jedoch müssen die Trainingsmuster so sortiert werden,dass bestimmte Muster, die zwar selten auftreten, aber dennoch wichtig sind,gut genug gelernt werden können. Diese Selektierung würde Zeit in Anspruchnehmen und auch eine automatische Generierung der gewünschten Ausgaben ist problematisch: Welchen Zweck sollte dieser Vorgang haben? Die Ausgaben würden entweder nachbestimmten Kriterien ausgewählt werden, könnten also auch von Anfang an offlinegelernt werden, oder das NN soll sich an die Art des Spielens der Gegneranpassen. Um Letzteres zu ermöglichen müssten auch Muster gefunden werden, diedem Bot Vorteile bringen könnten. Diese neuartigen, ‚kreativen’ Trainingsmusterkönnten vielleicht mit Hilfe eines evolutionären Algorithmus, also mit Hilfevon Mutationen und Kreuzungen meist erfolgreicher Bots, gewonnen werden. Einevolutionärer Algorithmus benötigt auch immer eine sogenannte Fitnessfunktion,die die Fähigkeiten des Bots bewertet. Als Möglichkeit wäre anzunehmen, dassder Wert der Fitnessfunktion von der Anzahl der Frags und der Anzahl der eigenenTode abhängt. Ein solcher Ansatz ist aber bei Counterstrike nicht aussagefähig,weil dort zum einen das Erreichen des Missionsziels hinzukommt, zum anderenauch keine einfache Bewertung der Frags aufgrund der vielen verschiedenenEigenschaften der verschiedenen Waffen möglich ist. Am ehesten wäre eineBewertung aufgrund des Ergebnisses mehrerer Runden zu machen um Kreuzungen zusteuern. Da eine Runde bis zu 5 Minuten dauert, ist ein solcher Ansatz nichtpraktikabel, weil oft mehr als 50 Generationen entwickelt werden müssen, biseine merkliche Verbesserung der Eigenschaften des Agents zu beobachten ist. [PfScheier99]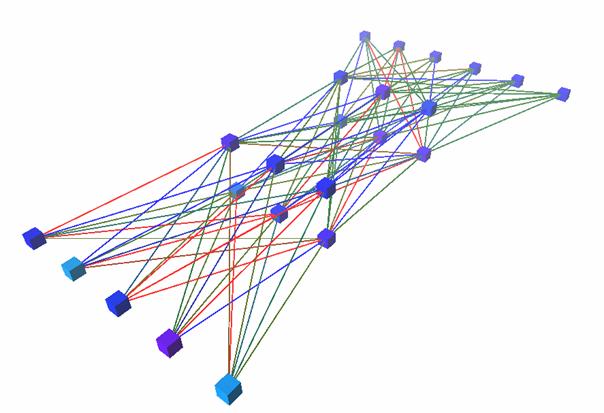
Abbildung14 : Kampf-NNdes Bots (6-6-6-5)
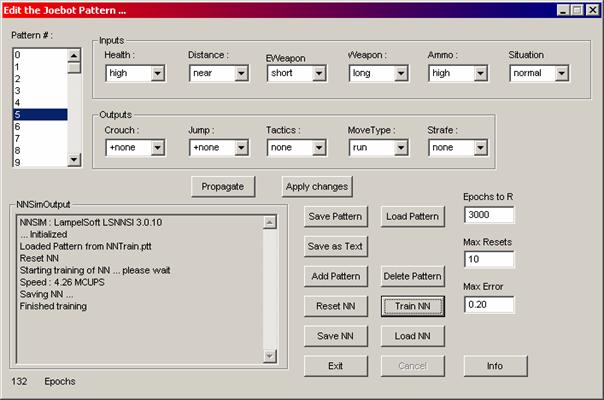
Aufgrundder oben genannten Schwierigkeiten habe ich mich bei diesem Bot für eineinfaches NN für die Kampfentscheidungen entschieden, dass offline trainiertwird. Zurzeit hat das Netz eine Größe von 6-6-6-5 und wird mit demunmodifizierten Lernverfahren Backpropagation trainiert. Das Netz zurVermeidung von Kollisionen ist ein 3-3-1 Feedforward-Netz.
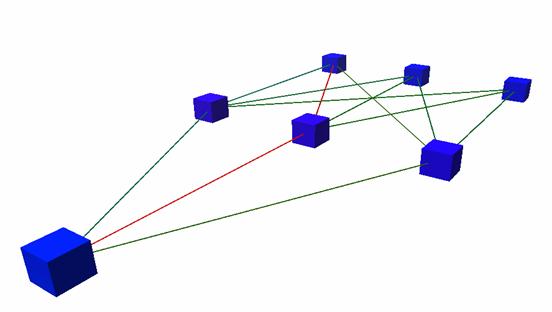
Abbildung 15 : Kollisions- NN desBots (3-3-1)
Abbildung 16 : Die 3 'Fühler' desBots, die die Daten für das Kollisionsnetz sammeln. (Hier sind auch die‚Fühler’ aus vorherigen Frames sichtbar.)
Zeitweisehabe ich versucht, das neuronale Netz während des Spiels mit Daten aus demSpiel zu trainieren. Wenn ein Bot bspw. gegen einen Gegner gewonnen hatte odermit dem Leben davongekommen war, so trainierte ich das Netz mit den Eingabe undAusgabedaten der letzten maximal 2 Sekunden, wobei die Ausgabedaten verstärktwurden, d.h. wenn eine Ausgabe den Wert 0.8 hatte, so wurde sie auf 1.0gesetzt. Für diesen Zweck verwendete ich ein größeres Netz ( 5-10-10-5 ), um zuermöglichen, dass das Netz mehr verschiedene Situationen lernen kann. Wenn ichdas mit den offline gewonnenen Trainingsdaten trainierte Netz als Ausgangsnetzverwendete, so kam es vor, dass die Bots anfingen sehr defensiv zu spielen – siewurden ja immer ‚belohnt’, wenn sie überlebten – oder es kam auch vor, dass dieAktivierung der Ausgabeneuronen immer nahe Null lag, und diese auch nicht mehrstark von der Aktivierung der Eingabeneuronen abhing, obwohl dieVerbindungsgewichte nicht alle gleich 0 waren, sondern die Signale sichaufhuben. Dies war vor allem der Fall, wenn das Netz bei dem Tod eines Botsdessen Trainingsdaten verlernen sollte. ( Dem Netz wurden die Eingabedaten unddie inversen Ausgabedaten zum Lernen repräsentiert. Als Lernverfahren fandBackpropagation Anwendung, was eigentlich ja nicht für diesen Zweck gedachtwar). Auch mit einem zufälligen Netz war auch nur eine Konvergenz derAusgabedaten gegen 0 zu beobachten.
